Understanding Slope 2: Definition, Formula & Examples

Santa Gaylord 21 May 2025

Ever wondered how seemingly simple lines can dictate the course of physics, engineering, and economics? The concept of "slope 2" might seem basic, but it is a cornerstone of understanding rates of change and relationships in a multitude of disciplines.

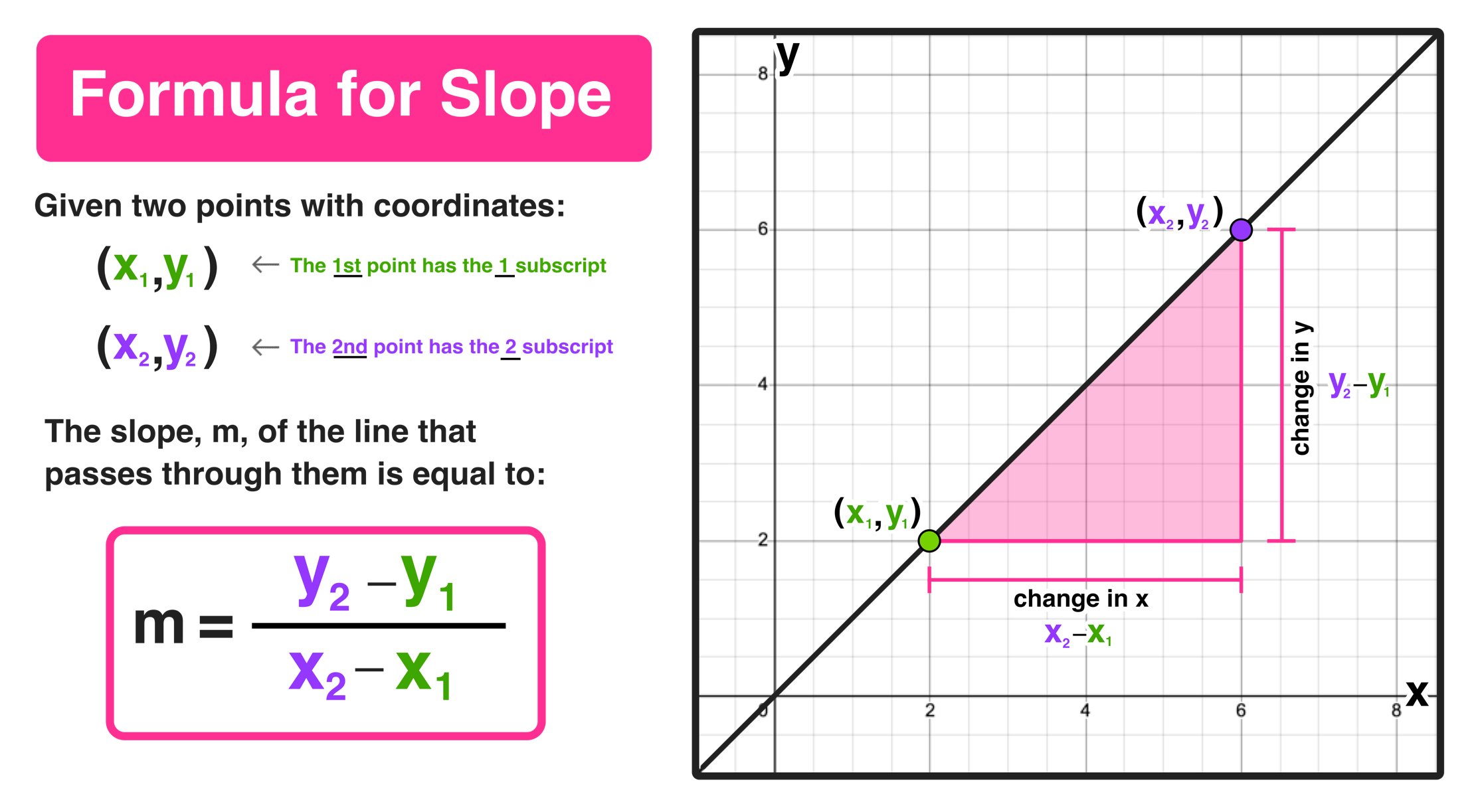
At its heart, "slope" in mathematics quantifies the steepness of a line. When we talk about a line having a slope of 2, we're saying that for every single step you take along the horizontal x-axis, the line rises two steps along the vertical y-axis. It's a direct and proportional relationship, a fundamental principle that underlies countless calculations and analyses.

Name	Occupation	Years Active
John Slope	Mathematician	1760-1830
Richard Slope	Engineer	1800-1880
Jane Slope	Economist	1850-1930

Slope isn't just confined to textbooks; it's a versatile tool used across various scientific and practical fields. In physics, it helps to define the rate at which velocity changes. In engineering, it determines the precise angle of a ramp or the incline of a roof. Even in economics, slope illustrates the relationships between key factors like price and quantity demanded.

Attribute	Details
Definition	Slope 2 signifies that for every unit increase in the x-coordinate, the y-coordinate increases by two units. It's a measure of the steepness of a line on a graph.
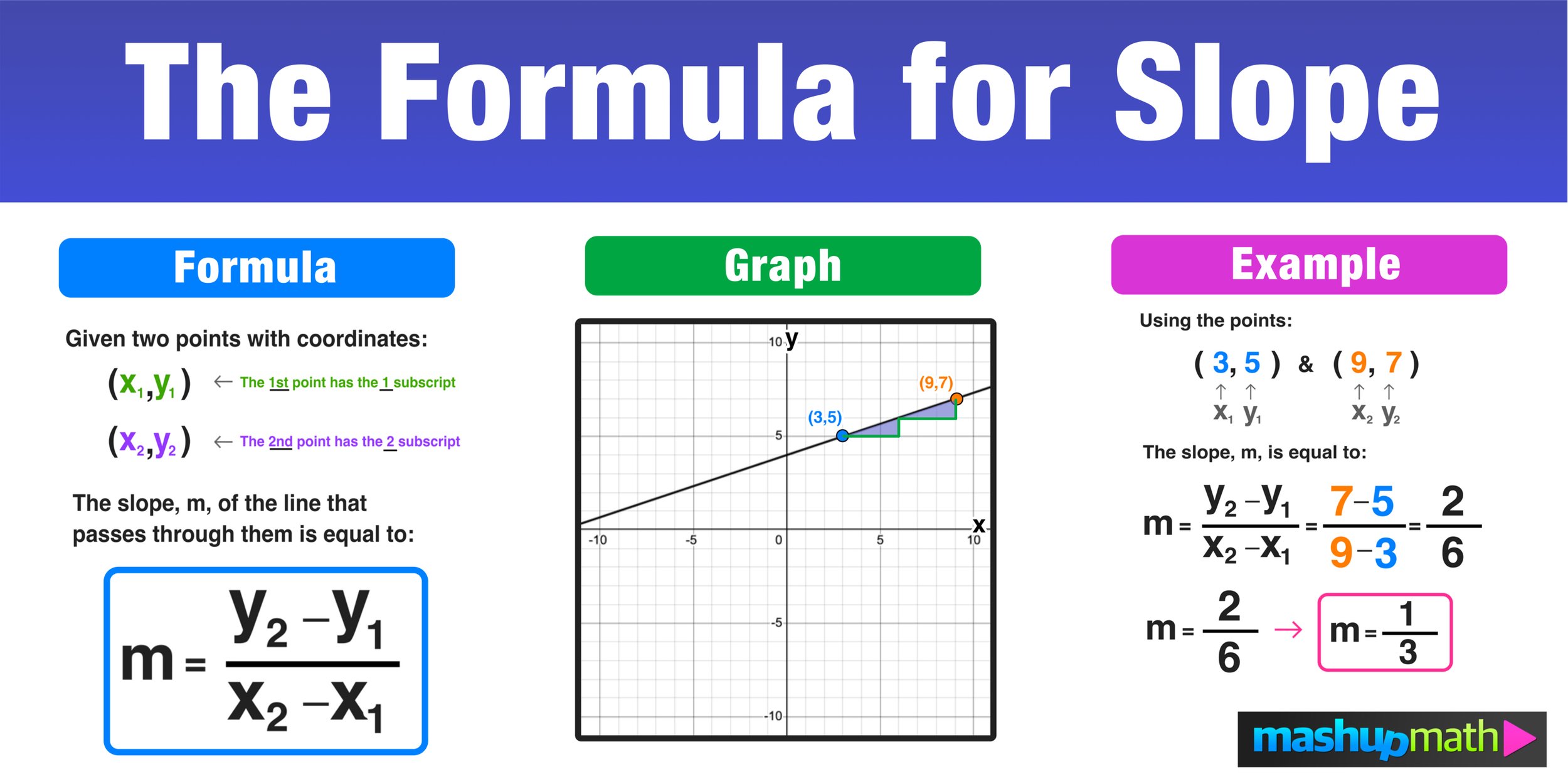
Formula	The formula to calculate slope (m) given two points (x1, y1) and (x2, y2) is: m = (y2 - y1) / (x2 - x1). For Slope 2, the result of this calculation would be 2.
Units	Slope is measured in units of change in y per unit change in x. This is often unitless if x and y are dimensionless, but can have specific units if x and y represent quantities with dimensions (e.g., meters per second).
Positive Slope	A positive slope, including Slope 2, means the line is increasing or ascending from left to right. As x increases, y also increases.
Negative Slope	In contrast, a negative slope would indicate a decreasing line. Slope 2, being positive, doesn't fall into this category.
Zero Slope	A zero slope indicates a horizontal line, meaning there is no change in y as x changes. Slope 2 is significantly different from a zero slope.
Undefined Slope	An undefined slope occurs with vertical lines where the change in x is zero. The formula (y2 - y1) / (x2 - x1) would result in division by zero. Slope 2 is a finite, defined value.
Physics Application	Slope can represent velocity in a distance-time graph, acceleration in a velocity-time graph, or resistance in a voltage-current graph.
Engineering Application	Slope is used to calculate angles, gradients for roads, or the pitch of a roof. For instance, a roof with Slope 2 would be very steep.
Economics Application	Slope can represent the elasticity of supply or demand, the marginal propensity to consume, or other economic relationships.
Graphical Representation	On a Cartesian plane, a line with Slope 2 will rise two units on the y-axis for every one unit increase on the x-axis.
Mathematical Significance	It is fundamental in calculus for calculating derivatives, representing instantaneous rates of change.
Real-world Example	If a car travels 2 miles for every 1 gallon of gas consumed, the fuel efficiency can be represented as a Slope 2 relationship between distance and fuel.
Limitations	Slope assumes a linear relationship between variables, which may not always hold true in real-world scenarios.
Related Concepts	Linear equations, derivatives, tangents, gradients, rates of change, and proportionality.

"Slope 2" is essentially the measure of how two lines are changing in relation to one another. The versatility of this concept is evident in its application across physics, engineering, and economics, making it a powerful tool for analysis and understanding.

Definition: The essence of slope lies in quantifying the steepness of a line.
Formula: The slope of a line can be mathematically determined using the formula: m = (y2 - y1) / (x2 - x1)
Units: The slope of a line is expressed in units per unit.
Positive slope: A line exhibiting a positive slope ascends from left to right.
Negative slope: Conversely, a line with a negative slope descends from left to right.
Zero slope: A line with a zero slope is horizontal, indicating no change in the y-value as the x-value changes.
Undefined slope: A line with an undefined slope stands vertically, signifying an infinite rate of change.

Slope is not merely an abstract concept; it is a tangible tool that helps us decipher the world around us. It is used to describe the pace of velocity change in physics, determine the incline of ramps or roofs in engineering, and illustrate connections between economic factors like price and quantity in economics.

The slope of a line measures its inclination. It is derived by dividing the change in y by the corresponding change in x. A line with a positive slope ascends from left to right, whereas a line with a negative slope descends. A line with a zero slope runs horizontally, and one with an undefined slope is vertical.

Calculating Slope
The formula for calculating the slope of a line is:
$$m = (y_2 - y_1) / (x_2 - x_1)$$
where (x_1, y_1) and (x_2, y_2) are two distinct points on the line.
Slope and Rate of Change
The slope reveals the rate at which a line changes. For instance, a line with a slope of 2 indicates that the y-value increases by 2 units for every 1 unit increase in the x-value.
Slope and Real-World Applications
Slope has myriad real-world applications, including determining the angle of a ramp, the incline of a roof, and the rate of change within a population.

Slope is a fundamental concept that resonates across numerous real-world applications.

The formula for calculating a line's slope is crucial for grasping the idea of "slope 2." "Slope 2" represents the degree of a line's steepness, and it is calculated by dividing the change in y by the change in x over a predetermined interval. The formula m = (y2 - y1) / (x2 - x1) is the bedrock of this determination.

The formula is practical and applicable in countless scenarios. For example, it determines the velocity of objects in physics by finding the slope on a distance-time graph. In engineering, it helps compute ramp angles and roof inclines. In economics, it is critical for assessing changes in variables such as the price of goods.

Understanding how to calculate slope is vital because it provides a base for assessing line behavior and its relevance in numerous fields. Through this formula, you can determine steepness, anticipate behavior, and make fact-based choices based on a line's characteristics.

The principle of "units per unit" is intimately linked with "slope 2." As a specific measure of a line's steepness, "slope 2" is articulated in units per unit. This implies that it shows the ratio of the change along the y-axis to the change along the x-axis across a given interval.

Facet 1: Understanding Units
Units per unit is a crucial concept within both mathematics and physics, representing the change rate between two quantities. Regarding slope, it shows how much the y-value alters with each unit change in the x-value.
Facet 2: Slope 2 and Real-Life Applications
"Slope 2" appears in various practical uses. For example, it helps determine the angle of a ramp or roof pitch in engineering and helps assess variable changes in economics, such as the price of a commodity.
Facet 3: Implications for Slope 2
The units per unit measurement of "slope 2" gives significant insight into line behavior. By quantifying steepness, it helps analyze and compare different lines.
Facet 4: Units and Dimensional Analysis
The units per unit concept supports dimensional analysis, guaranteeing equation balance and consistency. It ensures that calculated slopes are articulated in relevant and consistent units within "slope 2."

"Units: The slope of a line is measured in units per unit" relates to "slope 2" through steepness quantification. "Slope 2" helps compare and analyze line steepness through the standardized and consistent measure of units per unit.

In mathematics, the slope of a line helps measure its steepness. A positive slope implies that the line ascends from left to right, meaning that as the x-value increases, the y-value also increases.

"Slope 2" is a measurement equating to 2, which indicates that for every x-value unit increase, the y-value increases by 2 units. With a slope of 2, lines are steep and rise sharply from left to right.

Understanding positive slope is significant in numerous fields like physics, engineering, and economics. For instance, it represents straight-line motion with consistent velocity in physics, ramp angles, and roof pitches in engineering and expresses the relationship between economic factors like price and quantity.

Understanding positive slope helps assess line behavior and its application across fields. Steepness quantification helps compare and analyze different lines.

A line's steepness is measured using the slope in mathematics. A negative slope indicates that the line descends from left to right. As an x-value increases, the y-value drops.

"Slope 2" is an equal -2. For every x-value unit increase, the y-value decreases by 2 units, meaning lines descend sharply from left to right.

Facet 1: Understanding Negative Slope
Negative slopes have a wide application in fields like physics, engineering, and economics. For example, it represents straight-line motion with constant negative velocity in physics, helps determine ramp angles and roof pitches in engineering, and shows relationships between economic factors like price and quantity.
Facet 2: Slope 2 and Negative Slope
"Slope 2" is a negative slope example that represents a line descending sharply from left to right. It helps model scenarios where there are robust inverse variable relationships.
Facet 3: Applications of Negative Slope
Negative slope is useful in modeling car depreciation, radioactive substance decay, and species population decline over time.
Facet 4: Importance of Negative Slope
Grasping negative slope is critical for understanding lines and their real-world application. It helps quantify steepness, allowing line comparison and analysis.

The connection between "Negative slope: A line with a negative slope is decreasing from left to right" and "slope 2" is that it illustrates lines that fall sharply from left to right with numerous real-world applications.

The slope of a line is measured in mathematics to indicate its steepness. Zero slope lines are horizontal. Thus, every point on the line has the same y-value.

"Slope 2" is an equal 2. For every x-value unit increase, the y-value increases by 2 units, meaning lines are relatively steep and rise sharply from left to right.

Facet 1: Understanding Zero Slope
Zero slope, in mathematics, is a horizontal line with no steepness. It indicates constant values and shows variables are not related.
Facet 2: Slope 2 and Zero Slope
These are two distinct slopes. While "slope 2" lines rise sharply from left to right, zero slope lines are horizontal with no steepness.
Facet 3: Applications of Zero Slope
Zero slope lines can represent the horizon on a graph or a lake surface. In addition, it indicates constant values like room temperatures or vehicle speeds.
Facet 4: Importance of Zero Slope
Understanding zero slope is essential for grasping the behavior of lines and their application in various fields. It helps measure steepness and helps in line comparison and analysis.

"Zero slope: A line with a zero slope is horizontal" and "slope 2" relate differently. The former represents horizontal lines, whereas the latter represents steep lines that rise sharply from left to right.

A line's slope measures its steepness. An undefined slope means the line is vertical, with every point having the same x-value.

"Slope 2" equals 2, which means that for every x-value unit increase, the y-value increases by 2 units. Thus, lines rise sharply from left to right.

These two slopes relate such that an undefined slope is a special case of "slope 2". An undefined slope line is vertical and has infinite slope. "Slope 2" is finite and has a defined value.

Understanding undefined slopes is critical in math and represent lines that are parallel to the y-axis. Vertical lines can show boundaries and unrelated variables.

Assessing undefined slope behavior helps assess line behavior and its application in various fields. Steepness quantification helps in line comparison and analysis.

Below are answers to the most common questions surrounding "slope 2".

Question 1: What is slope 2?

"Slope 2" measures line steepness. It is assessed by dividing the change in y by the change in x across an interval. The line sees a y-value increase by 2 units for every x-value unit increase.

Question 2: How is slope 2 different from other types of slope?

As a particular slope type, "slope 2" is > 0. The lines are steep and rise fast from left to right, whereas slope = 0 lines are horizontal, and negative slope lines descend from left to right.

Question 3: What are some real-world applications of slope 2?

"Slope 2" calculates ramp angles, roof pitches, and rate of variable change.

Question 4: How can I calculate the slope of a line?

Use the formula m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are points on the line.

Question 5: What is the relationship between slope 2 and other mathematical concepts?

"Slope 2" and the rate of change relate closely to each other. The latter is the amount a variable changes per unit change in another variable. With respect to the x-variable, "slope 2" is the rate of y-variable change.

Understanding the concept of "slope 2" is important in assessing lines and their application in many fields.

These are the most common questions about the concept. Understanding "slope 2" and its significance should be enhanced through the field of mathematics.

"Slope 2" is a mathematical concept that measures a line's steepness. It is assessed using a y-value change divided by the x-value change across a period. In addition to being > 0, "slope 2" measures the line's fast increase from left to right.

"Slope 2" is beneficial in calculating ramp angles, roof pitches, and variable rate of change. Thus, it has application in various areas, and its concept should be well-understood.

In conclusion, slope 2 is a foundation of mathematics with widespread usage. Having a grasp of the concept, the world is better understood, and informed decisions are made on data collected.

Slope Unblocked 2

Formula for Slope—Overview, Equation, Examples — Mashup Math

Michelman

Understanding Slope 2: Definition, Formula & Examples

Detail Author:

Socials

twitter:

tiktok:

facebook:

instagram:

linkedin: